Imagínese participar en una competición televisada donde ganar el coche es el premio. Hay tres puertas cerradas frente a ti: detrás de una hay un automóvil y detrás de la otra dos cabras. Para ganar el coche, debes adivinar qué puerta está detrás. Y podría ser cualquiera de esos tres.
El anfitrión te pide que elijas uno. Él lo hace. Después de eso, abre una de las puertas no elegidas y revela la cabra. Luego viene la pregunta crucial: ¿quieres mantener tu elección o cambiar a otra?
La mayoría de la gente piensa que no importa: inicialmente, con tres puertas, la probabilidad de esconder un coche era 33–33–33; Ahora que hay dos, nos queda 50–50. Pero no es así.
El coche tiene 1/3 de posibilidades de estar detrás de la puerta elegida por el jugador. Las otras dos puertas tienen probabilidad 2/3. Joaquin Cordova / Wikimedia Commons., CC BI Ilusiones estadísticas
Este pequeño juego se llama el problema de Monty Hall, en honor al presentador del programa de televisión estadounidense Let’s Make a Deal. El problema fue planteado y resuelto por el matemático Steve Selwyn en 1975. Y se ha convertido en uno de los acertijos más famosos de la estadística, porque desafía nuestra intuición de una manera casi desagradable.
A veces se lo describe como una ilusión estadística, incluso en publicaciones especializadas, debido a la distancia entre lo que creemos que debería suceder y lo que realmente sucede.
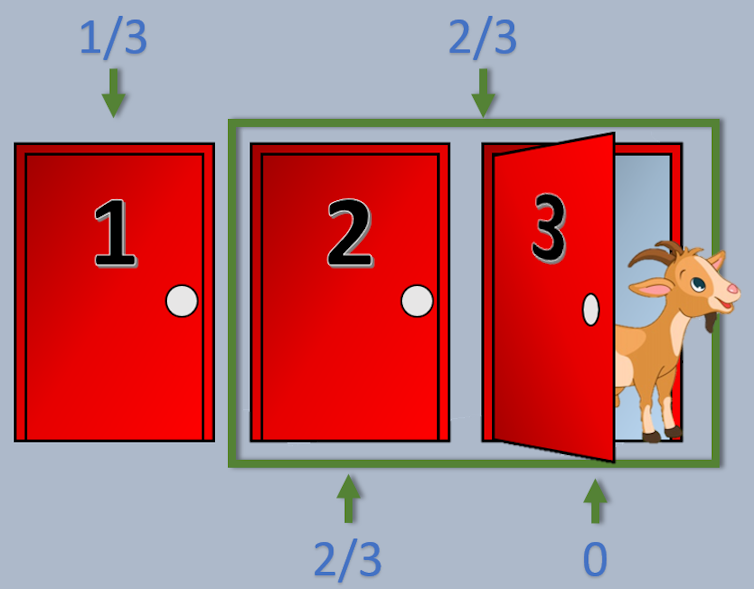
Cuando el anfitrión abre la puerta, las probabilidades para los dos conjuntos no cambian, pero las probabilidades cambian a 0 para la puerta abierta; y 2/3 para puertas cerradas (2). Joaquín Córdova / Wikimedia Commons., CC BI
Lo fascinante es que detrás de esta decisión aparentemente trivial está el hecho de que cuando recibimos nueva información –aunque parezca irrelevante– nuestras probabilidades cambian, incluso si no siempre sabemos cómo actualizarlas correctamente. Entramos en el ámbito de las matemáticas, la probabilidad condicional y el teorema de Bayes, donde todo se vuelve menos intuitivo.
Sin embargo, podemos explicarlas sin necesidad de todo esto: la lógica, la proporcionalidad y el sentido común bastan para entender por qué la elección del presentador ha inclinado claramente la balanza, y una de las puertas promete más que las demás a la hora de ocultar el coche.
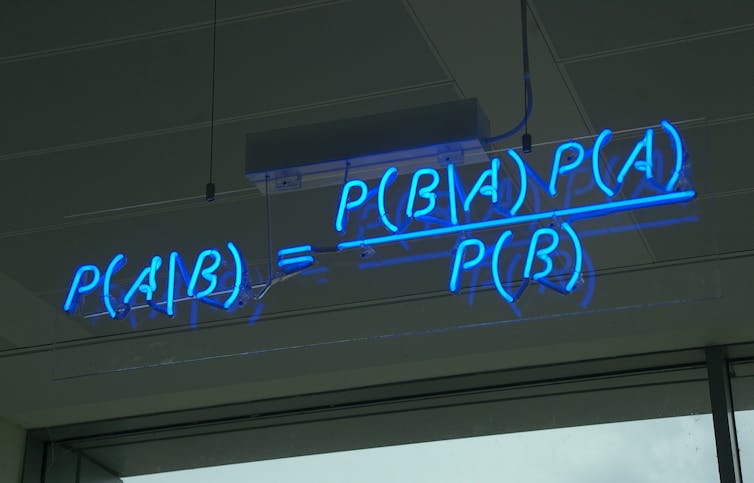
Declaración del teorema de Bayes. Mattbuck / Wikimedia Commons., CC BI Explicación
Suponemos que el concursante eligió la puerta A, aunque el razonamiento sería exactamente el mismo si eligiera la B o la C.
Si el concursante ha elegido la puerta A, entonces le toca al anfitrión quien puede abrir la puerta B o C, siempre con la única condición de que no se muestre el coche, para mantener el enigma de su ubicación, que es la clave del juego.
Supongamos que abre B, abrir C conduciría exactamente al mismo punto. Por tanto, hay dos opciones ya que B está desactivado:
Si el coche está en A, también podría abrir B o C (ambos tienen cabra). Por tanto, la probabilidad de que B abra no es del 100%, sino del 50% que comparte C.
Si el auto está en C, entonces la puerta B es la única que se puede abrir. En ese caso, la probabilidad de que B abra es del 100%. El doble que antes.
Esto implica que el hecho de que el presentador haya abierto B es más compatible con el escenario “el coche estaba en C” que con el escenario “el coche estaba en A”.
Por otro lado
Invertimos el razonamiento y pensamos en términos del competidor, que es quien debe tomar la decisión. Al observar que el presentador abrió B, y dado que esa acción es más probable cuando el automóvil está en C que cuando está en A, entonces se vuelve más probable para él que el automóvil esté en C que en A.
Por lo tanto, si es más probable que el auto esté en C, entonces cambiar a C aumenta la probabilidad de ganar, porque el comportamiento del presentador revela información que favorece ese escenario más que otros.
¿Hasta qué punto? Considerando que una es el doble de la otra (del 50% al 100%) y que no hay más opciones, para terminar con el 100% como suma de ambas nos queda una distribución del 33%-66% para las opciones A y C, respectivamente.
La intuición puede fallar
En la motivación del directivo, al abrir la puerta B, el hecho de que el coche esté detrás de la puerta C tiene más peso que detrás de la puerta A. Y, por tanto, es más probable que esté detrás de esa puerta. Esta es la razón por la que, si el concursante cambia de elección, las posibilidades de ganar son mayores.
Esta explicación se aplica si el concursante eligió A. Para las otras dos opciones, el enfoque es el mismo: si elige B, A se intercambia por B. Si elige C, A se intercambia por C.
Finalmente, el problema de Monty Hall nos recuerda que la intuición puede fallar, incluso en situaciones simples. Actualizar correctamente la información no sólo cambia el resultado: cambia nuestra comprensión de cómo funciona realmente la aleatoriedad.
Y aceptar esa idea, incluso si pone en duda lo que “nos parece lógico”, es una parte esencial para pensar mejor.
Descubre más desde USA TODAY NEWS INDEPENDENT PRESS US
Suscríbete y recibe las últimas entradas en tu correo electrónico.










